Asymptote

Le terme d'asymptote est utilisé en mathématiques pour préciser des propriétés éventuelles d'une branche infinie de courbe à accroissement tendant vers l'infinitésimal. C'est d'abord un adjectif d'étymologie grecque qui peut qualifier une droite, un cercle, un point… dont une courbe plus complexe peut se rapprocher. C'est aussi devenu un nom féminin synonyme de droite asymptote.

Une droite asymptote à une courbe est une droite telle que, lorsque l'abscisse ou l'ordonnée tend vers l'infini, la distance de la courbe à la droite tend vers 0.

L'étude du comportement asymptotique est particulièrement développé dans les études de fonctions et présente des commodités reconnues par de nombreux mathématiciens. Dans le domaine scientifique, il arrive fréquemment d'étudier des fonctions dépendant du temps (évolution de populations, réaction chimique ou nucléaire, graphique de température, oscillation d'un amortisseur). Un des objectifs du chercheur est alors de connaître l'état à la fin de l'expérience, c’est-à-dire lorsqu'un grand intervalle de temps s'est écoulé. L'objectif n'est alors pas de connaître les variations intermédiaires mais de déterminer le comportement stable, à l'infini du phénomène mesuré.

Le projet d'une définition uniforme n'étant pas raisonnable, cet article détaillera plusieurs situations.

Asymptote et rencontre

L'étymologie grecque du mot « asymptote » construit à l'aide du préfixe privatif « a » et de « symptôsis » (rencontre) laisse imaginer que deux courbes asymptotes ne se rencontrent pas. Cette impression est renforcée par certains usages littéraires du terme : Modèle:Citation – (Victor Hugo. William Shakespeare - L'art et la science ; cependant, si l'on suit l'usage du terme qui est fait en mathématiques, il faudrait plutôt dire : "la vérité est l'asymptote de la science", puisque l'asymptote est ce vers quoi une courbe se rapproche, c'est-à-dire en l'occurrence : la science tend vers la vérité, et non l'inverse). Une des premières rencontres de droites asymptotes avec l'étude de l'hyperbole semble confirmer cet état de fait. Cette condition de ne jamais se rencontrer est même présente dans les vieilles définitions de l'asymptote. Cependant, la définition mathématique actuelle du terme (courbes se rapprochant indéfiniment près l'une de l'autre) permet la rencontre des courbes une fois ou même une infinité de fois et n'exclut pas la possibilité que les courbes se trouvent confondues.

• 
  Courbe d'équation Modèle:Math et sa droite asymptote Modèle:Math : Modèle:Math. Courbe et droite se rencontrent pour Modèle:Math.
• 
  Courbe d'équation Modèle:Math et sa droite asymptote Modèle:Math : Modèle:Math. Courbe et droite se rencontrent une infinité de fois.
• 
  Courbe d'équation Modèle:Math (où Modèle:Math désigne la fonction partie entière) et sa droite asymptote Modèle:Math : Modèle:Math. Courbe et droite finissent confondues.
• 
  Courbe d'équation paramétrique Modèle:Math et sa droite asymptote (d) : Modèle:Math. Courbe et droite se rencontrent une infinité de fois.

Courbe d'équation Modèle:Math

Les asymptotes sont à rechercher lorsque Modèle:Mvar ou Modèle:Math tend vers l'infini.

Droite asymptote

Dans ce qui suit, on utilisera les notations Modèle:Mvar et Modèle:Mvar pour désigner des nombres réels, donc finis.

Asymptote « verticale »

Hyperbole, courbe représentative de la fonction inverse. Les deux axes (donc les droite Modèle:Math et Modèle:Math) sont des asymptotes à la courbe.

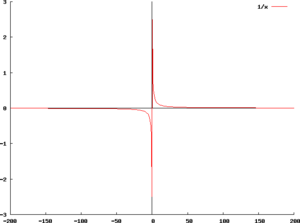
La droite d'équation Modèle:Mvar est une asymptote verticale à la courbe représentative de la fonction Modèle:Mvar (en Modèle:Mvar) si, plus la valeur de Modèle:Mvar se rapproche de la valeur finie Modèle:Mvar aussi près que l'on veut, en restant plus petite ou plus grande que Modèle:Mvar, mais sans jamais être égale à Modèle:Mvar, plus la valeur de Modèle:Math s'approche de l'infini :

$\lim _{x\to a}f(x)=\pm \infty .$

On trouvera des asymptotes verticales en particulier lorsque la fonction Modèle:Mvar se présente sous forme d'un quotient dont le dénominateur s'annule en Modèle:Mvar, mais pas le numérateur.

Exemples : fonction homographique, logarithme népérien, fonction tangente

Asymptote « horizontale »

La droite d'équation Modèle:Mvar est asymptote horizontale à la courbe d'équation Modèle:Math, si, lorsque Modèle:Mvar s'accroît autant qu'on veut vers l'infini (mais sans jamais atteindre l'infini), Modèle:Math s'approche d'une valeur finie Modèle:Mvar :

$\lim _{x\to \pm \infty }f(x)=b.$

Exemples : fonction homographique, fonction exponentielle, tangente hyperbolique

Asymptote « affine »

Courbe d'équation Modèle:Math, l'axe des Modèle:Mvar et la droite (d) : Modèle:Mvar sont toutes les deux des asymptotes à la courbe.

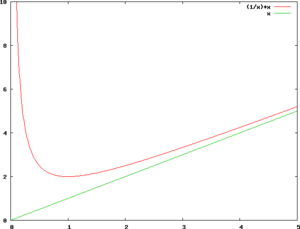
La droite d'équation Modèle:Mvar (Modèle:Mvar étant ici différent de 0) est asymptote oblique à la courbe représentative de la fonction Modèle:Mvar si $\lim _{x\to \pm \infty }\left(f(x)-ax-b)\right)=0.$

Les valeurs de Modèle:Mvar et de Modèle:Mvar se calculent à l'aide des formules suivantes :

$a=\lim _{x\to \pm \infty }{f(x) \over x}$ $b=\lim _{x\to \pm \infty }{f(x)-ax}$

Si $\lim _{x\to \pm \infty }{f(x) \over x}$ est égale au réel Modèle:Mvar alors que Modèle:Math n'admet pas de limite réelle en Modèle:Math, on dit que la courbe admet comme direction asymptotique la droite d'équation Modèle:Mvar.

Si $\lim _{x\to \pm \infty }{f(x) \over x}$ est égale au réel Modèle:Mvar et si $\lim _{x\to \pm \infty }f(x)-ax=\pm \infty$, on parle alors de branche parabolique de direction Modèle:Mvar.

Le point de vue projectif

Les trois situations précédentes n'en forment qu'une en géométrie projective, une asymptote étant une tangente à l'infini.

Courbe asymptote

Trident d'équation Modèle:Math et ses deux courbes asymptotes d'équation Modèle:Math et Modèle:Math.

La courbe d'équation Modèle:Math est asymptote à la courbe d'équation Modèle:Math en Modèle:Math si $\lim _{x\to \pm \infty }f(x)-g(x)=0$ . Les asymptotes « horizontales » ou « obliques » sont alors des cas particuliers de courbes asymptotes de ce type.

Courbe paramétrée

Droite asymptote

On cherche les droites asymptotes aux branches infinies de la courbe d'équation Modèle:Math, c’est-à-dire en Modèle:Math (réel ou infini) tel que $\lim _{t\to t_{0}}OM(t)=+\infty$ où Modèle:Math est le point de coordonnées Modèle:Math.

La droite d'équation Modèle:Math est asymptote à la courbe en Modèle:Math si

$\lim _{t\to t_{0}}OM(t)=+\infty \ \mathrm {et} \ \lim _{t\to t_{0}}ax(t)+by(t)+c=0$.

Pour rechercher une droite asymptote à la courbe, on observe si l'une ou l'autre des coordonnées tend vers l'infini quand Modèle:Mvar tend vers Modèle:Math. Si aucune des coordonnées ne tend vers l'infini, on ne recherche pas de droite asymptote.

Si l'une des coordonnées tend vers l'infini tandis que l'autre tend vers un réel, on peut conclure sur l'existence d'une asymptote :

• la courbe admet la droite Modèle:Math pour asymptote en Modèle:Math si :

  $\lim _{t\to t_{0}}x(t)=+\infty \ \mathrm {et} \ \lim _{t\to t_{0}}y(t)=y_{0}$ ;

• la courbe admet la droite Modèle:Math pour asymptote en Modèle:Math si :

  $\lim _{t\to t_{0}}x(t)=x_{0}\ \mathrm {et} \ \lim _{t\to t_{0}}y(t)=+\infty$.

Dans le cas où les deux coordonnées tendent vers l'infini, on recherche une asymptote oblique. On cherche la limite de Modèle:Math quand Modèle:Mvar tend vers Modèle:Math. Si cette limite est égale à un réel Modèle:Mvar non nul, on cherche alors la limite de Modèle:Math quand Modèle:Mvar tend vers Modèle:Math. Si cette limite est égale à un réel Modèle:Mvar, alors la droite d'équation Modèle:Mvar est asymptote à la courbe. Dans tous les autres cas, il n'y a pas d'asymptote oblique.

Exemple : Considérons la courbe d'équation paramétrique

${\begin{cases}x(t)=1/(1-t^{2})\\y(t)=t^{3}/(1-t^{2})\end{cases}}$.

Lorsque Modèle:Mvar s'approche de –1, l'abscisse et l'ordonnée tendent vers l'infini, le rapport Modèle:Math tend vers -1 et la somme Modèle:Math tend vers 3/2 donc la courbe possède une droite asymptote d'équation Modèle:Math. La courbe possède également une asymptote (correspondant au cas où Modèle:Mvar tend vers 1) d'équation Modèle:Math ainsi qu'une dernière (cas où Modèle:Mvar tend vers l'infini) d'équation Modèle:Math.

Courbe d'équation polaire

On cherche les asymptotes à la courbe d'équation Modèle:Math lorsque Modèle:Mvar ou Modèle:Mvar tend vers l'infini ou une valeur donnée.

Droite asymptote

Une courbe d'équation polaire admet une direction asymptotique lorsque, pour Modèle:Math donné, on a

$\lim _{\theta \to \theta _{0}}\rho (\theta )=\infty$

La courbe admet alors une droite asymptote s'il existe un réel Modèle:Math tel que

$\lim _{\theta \to \theta _{0}}\rho (\theta )\sin(\theta -\theta _{0})=\lambda$

La courbe s'approche de la droite d'équation

$\rho (\theta )={\frac {\lambda }{\sin(\theta -\theta _{0})}}$

Cercle asymptote

La spirale d'équation Modèle:Math tend vers le cercle de rayon 1 par l'intérieur.

Une courbe d'équation polaire admet un cercle asymptote lorsqu'il existe Modèle:Math donné tel que

$\lim _{\theta \to \infty }\rho (\theta )=\rho _{0}$

La courbe « s'enroule » alors sur le cercle d'équation Modèle:Math.

Si au voisinage de Modèle:Math, Modèle:Math, la courbe s'enroule à l'intérieur du cercle asymptote, si, au contraire, au voisinage de Modèle:Math, Modèle:Math, alors elle s'y enroule à l'extérieur.

Point asymptote

Une spirale logarithmique tend vers un point asymptote.

Il peut arriver qu'une branche infinie d'une courbe s'enroule autour d'un point en s'en approchant indéfiniment. Ce point est alors appelé point asymptote à la courbe. On trouve cette situation au centre d'une spirale logarithmique. En équation polaire, l'origine est un point asymptote si $\lim _{\theta \to \infty }\rho (\theta )=0$.

Articles connexes

• Comparaison asymptotique
• Fonction asymptotique